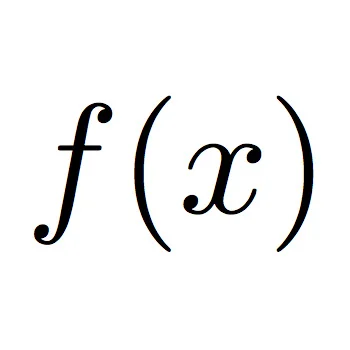Un outil mathématique incontournable - la fonction

Cet article est le premier d'une série d'articles mathématiques qui me permettront de détailler le fonctionnement de plusieurs outils mathématiques très utiles en physique. C'est aussi l'occasion de montrer qu'il y a bien une cohérence entre ces outils, qu'on peut les utiliser pour en bâtir de nouveaux. Je précise d'avance aussi que je n'aurai pas une rigueur de mathématicien. Mon but est de présenter assez simplement ces outils et comment ils permettent d'aller plus loin, ainsi que leur utilité en physique. Ici, je m'attarde sur la notion de fonction, une notion de base qui donne naissance à toute une branche des mathématiques, l'analyse.

Une fonction, qu'est-ce que c'est ?

Une fonction f, c'est une action, un mode d'emploi, une recette à appliquer à un nombre pour en obtenir un autre. f peut être par exemple « multiplier par 2 et ajouter 1 ». Appliquée au nombre 3, elle donne 7. On écrit donc f(3) = 7. Si l'on dispose d'une inconnue x, f(x) est un nombre et vaut 2x+1. La signification de f(x) est donc claire : c'est un nombre, et pour l'obtenir je prends le nombre x et je lui applique la recette « multiplier par 2 et ajouter 1 ». Qu'est-ce qu'elle apporte ?

– C'est un tout nouvel objet mathématique. Lorsque vous n'avez que les nombres, vous ne pouvez raisonner que sur les nombres, établir leurs propriétés. Si vous avez les fonctions, alors vous pouvez commencer à explorer les propriétés des « recettes » de nombres elles-mêmes. Par exemple, on peut trouver des fonctions g paires, si pour n'importe quel nombre x, g(-x)=g(x). Connaître cette propriété pour une fonction que l'on utilise peut permettre des simplifications de calcul ou de raisonnement.

– Elle met en avant le lien qui peut unir plusieurs quantités. Par exemple, le volume V d'une sphère dépend de son rayon r. Le volume est donc une fonction V(r).

– Elle possède une représentation graphique. Pour cela, on trace une courbe représentative, dont chaque point correspond à la valeur que possède la fonction pour la valeur choisie de sa variable. Cette représentation permet d'avoir une vue d'ensemble des valeurs prises par la fonction, de la façon dont elle évolue, de là où elle atteint des valeurs particulières. Bref, elle facilite généralement la perception que l'on se fait d'une fonction.

– Elle peut permettre d'améliorer la lisibilité d'une équation. Le volume d'une sphère en fonction du rayon est donnée ci-contre, et s'il intervient dans une équation assez compliquée, le remplacer simplement par « V(r) » permet d'en alléger l'écriture sans en perdre de vue la signification des différents termes qui la composent.

Nous disposons donc maintenant d'un outil mathématique permettant l'étude des « recettes » de nombres. Dans certaines situations, on étudie une quantité (la vitesse d'une voiture par exemple) et on s'intéresse à l'évolution de cette quantité par rapport à un paramètre (l'évolution de la vitesse au cours du temps, ce qu'on appelle l'accélération). Comment remonte-t-on à cette évolution d'un point de vue mathématique ? C'est l'objet du prochain article, et bien sûr, les fonctions seront utiles !